False sharing

• Cache ping-pong

std::hardware_destructive_interference_size

还有 std::hardware_constructive_interference_size。在大多数情况下这两个值相等，而且都等于 cache line 的大小。

https://stackoverflow.com/questions/39680206/understanding-stdhardware-destructive-interference-size-and-stdhardware-cons 第一个回答的评论里面指出如果目标平台有多个，那么为了兼容性，这两个常量可能是不同的。在特定架构上这两个常量应该是相同的。

例子：矩阵计算

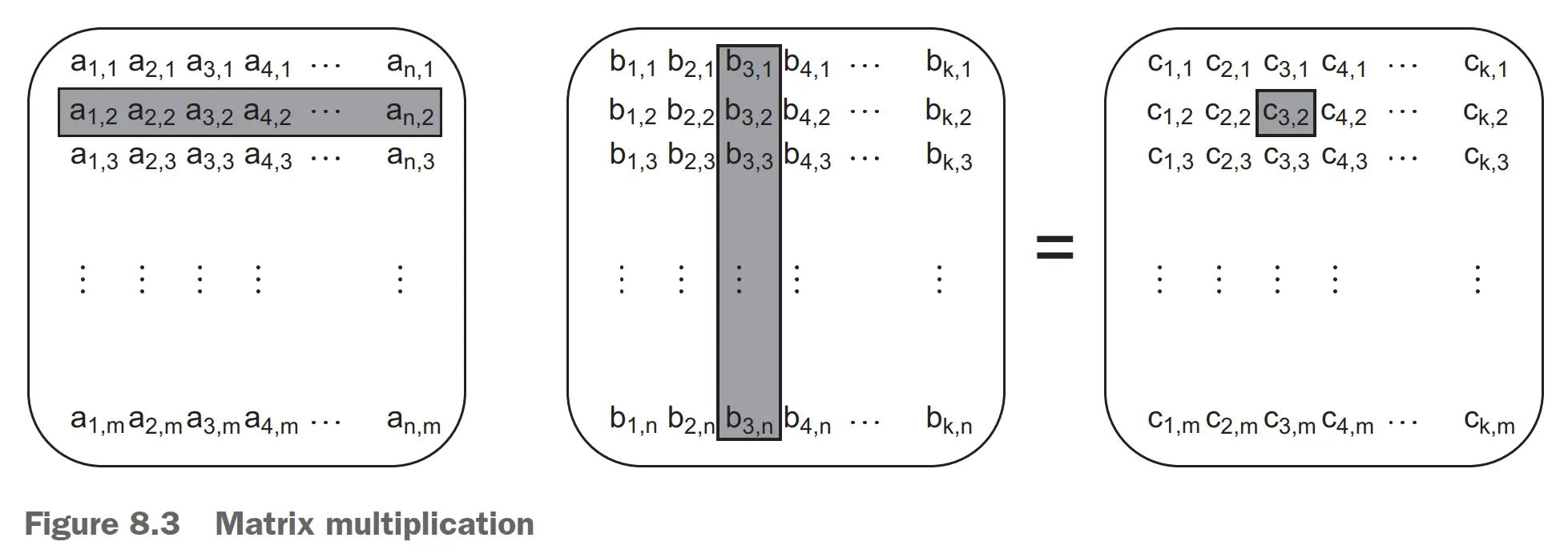
1. 每个线程计算一组列。列可以先加载到当前线程，每次都读一整行，对 cache 友好。
2. 每个线程计算一组行。相比于方案 1，读的 false sharing 更多，但是写操作的 false sharing 会更少。
3. 分块矩阵。访问输入矩阵元素的数量减少了，同时保持计算出来的元素数相同，因而效率更高。

Data access patterns in other data structures

例：树状结构

树状结构结点小，不同线程如果访问不同结点，cache line 重叠概率小，对 false sharing 有利。

例：Mutex

Mutex 和受保护数据在同一个 cache line 时，其他线程尝试上锁对持有锁的线程性能有影响。

Mutex locks are typically implemented as a read-modify-write atomic operation on a memory location within the mutex to try to acquire the mutex, followed by a call to the operating system kernel if the mutex is already locked.

当 mutex 和受保护数据要存在一起时，可以在数据结构中增加 padding 以隔开两者。

struct protected_data
{
    std::mutex m;
    char padding[std::hardware_destructive_interference_size];
    my_data data_to_protect;
};

或者像 cppreference 这样对要区分的两段数据用 alignas：

struct keep_apart
{
    alignas(std::hardware_destructive_interference_size) std::atomic<int> cat;
    alignas(std::hardware_destructive_interference_size) std::atomic<int> dog;
};

除了 hardware_destructive_interference_size 和 hardware_constructive_interference_size 暗示了 cache line 的大小之外，在 Linux 下我们还能用 /sys 文件系统下的信息得到 cache line 大小：

(base) ➜  main cat /sys/devices/system/cpu/cpu0/cache/index0/coherency_line_size
64

Exception safety in parallel algorithms

std::terminate()

By contrast, in a parallel algorithm many of the operations will be running on separate threads. In this case, the exception can’t be allowed to propagate because it’s on the wrong call stack.

如果不正确处理多线程环境下的异常，任何线程抛出未处理的异常都会导致 std::terminate() 被调用，整个进程被终止，见 https://godbolt.org/z/czPe8dbe8 。输出可能像这样：

terminate called after throwing an instance of 'std::runtime_error'
  what():  Exception from Thread B
Program terminated with signal: SIGSEGV

std::terminate() 会先打印当前的异常，再退出程序。如果当前没有异常，控制台输出可能为：

terminate called without an active exception
Program terminated with signal: SIGSEGV

这其实是默认的 terminate handler 做的事情，它先打印异常再调用 std::abort()，代码可参考 GCC 源码的 libstdc++-v3/libsupc++/vterminate.cc。我们也可以修改 terminate handler，它是一个全局的 handler，而且 set_terminate 和 get_terminate 都是线程安全的。

In any case, std::terminate calls the currently installed std::terminate_handler. The default std::terminate_handler calls std::abort. – https://en.cppreference.com/w/cpp/error/terminate

尽管能用 std::set_terminate 来修改 std::terminate_handler，但标准规定 handler 不能返回到 caller，否则未定义，所以一般只能做一些日志或清理操作，然后终止程序。

f shall terminate execution of the program without returning to its caller, otherwise the behavior is undefined. – https://en.cppreference.com/w/cpp/error/set_terminate

std::abort

std::abort（来自 cstdlib）通过 SIGABRT 信号终止程序，不会清理资源：

1. 析构函数不会被调用。
2. std::atexit() 和 std::at_quick_exit() 注册的函数不会被调用。
3. 文件等被打开的资源是否被关闭由实现定义。

虽然 C++ 标准没有说明如果 SIGABRT 信号被捕获是否还能终止程序，POSIX 标准说明了 abort() 会 override 对信号的阻塞或者忽略。C++ 标准说的是（C 语言标准类似）：

Causes abnormal program termination unless SIGABRT is being caught by a signal handler passed to std::signal and the handler does not return.

即如果 SIGABRT 被捕获了而且该信号处理器返回了，那么还是会强制终止程序。

从 C++ 标准 来看 std::abort 使用的信号是 SIGABRT，但是为什么退出时显示的信号是 SIGSEGV 呢？Reddit 帖子 说这个是 compiler explorer 沙盒的问题，我在 WSL 中重新尝试就确实看到了程序以 134 退出码结束（$128 + 6 = 134$，从 kill -l 中可以看到 6 号信号就是 SIGABRT）。

std::mem_fn

https://en.cppreference.com/w/cpp/utility/functional/mem_fn 给人一种可以把成员函数转换成 UFCS 的感觉。如果一个模板函数期望普通 unary 函数，而不会专门处理无参成员函数，那么可以将无参成员函数转换成普通 unary 函数，比如：

for_each(v.begin(), v.end(), mem_fn(&Item::Foo));

这样比自己写一个 lambda 更加简洁。

并行化 std::accumulate

用 std::packaged_task 保障异常安全

std::packaged_task 创建的线程会安全地处理异常，并将异常记录在 std::future 中，由 std::future 的获取这来处理。

The key thing to note for exception safety is that if you destroy the future without waiting for it, the destructor will wait for the thread to complete. This neatly avoids the problem of leaked threads that are still executing and holding references to the data.

书里面用了 join_threads 这个自定义的类，用来在离开作用域时检查给定 vector 中的 threads 是否 joinable()，如果是的话则发起 join()。这样可以防止在后面的代码用 std::future 获取结果时抛出异常，而有 std::thread 离开作用域还没有 join() 或 detach()，导致 std::terminate 被调用、程序终止。在 C++20 中可以用 std::jthread 来替代这种写法。

用 std::async 保障异常安全

用 std::async 来代替前面的 std::packaged_task 和 std::thread 的写法会更简单，而且可以避免忘记在发生异常离开当前作用域时对 std::thread 进行 join() 的问题（成书时还没有 std::jthread）。

使用 std::packaged_task 时，书上是预先划分了多个 chunk；在使用 std::async 时，书上是二分递归调用 std::async，因此代码进一步变得简洁。不是说 std::packaged_task 不能二分，只是书上只展示了这样的写法。

并行化 std::for_each

略。

并行化 std::find

用 std::thread + std::promise 实现

为了和标准库的接口一致，find 函数只需要一个结果，因此书上选择使用 std::promise 而不是 std::packaged_task。同样是创建一组线程，每个线程执行各自的搜索任务，但是现在不需要为每个线程都创建一个 future，只需要使用同一个 promise 与和它关联的一个 future。

书上是每个元素遍历前都检查一下所有线程可见的原子标志 done_flag，如果该标志为真则不再继续搜索。如果有线程先找到了元素或者出现了异常，这个 done_flag 都会被设置为真。我个人认为这个检查频率应该变小一点，不然容易影响搜索性能。

struct find_element
{
    void operator()(Iterator begin, Iterator end,
                    MatchType match,
                    std::promise<Iterator>* result,
                    std::atomic<bool>* done_flag)
    {
        try
        {
            for (; (begin != end) && !done_flag->load(); ++begin)
            {
                if (*begin == match)
                {
                    result->set_value(begin);
                    done_flag->store(true);
                    return;
                }
            }
        }
        catch (...)
        {
            try // 注意这里
            {
                result->set_exception(std::current_exception());
                done_flag->store(true);
            }
            catch (...)
            {
            }
        }
    }
};

每个线程找到结果或者发生异常之后都会尝试将结果写入 future，但是只有第一个线程能成功，其他线程会遇到异常。尤其是尝试 set_value() 的线程会遇到异常，从而进入下面 catch 块中并调用 set_exception()，但是这个调用依然会发生异常，因此外面还要包一层 try-catch。书上的代码通过双重 try-catch 简单处理了线程设置结果的数据竞争问题。

用 std::async 实现

前面用 std::thread + std::promise 实现是为了替代 std::thread + std::packaged_task。现在换成 std::async，不用专门使用 std::promise。每次进行二分后先检查前一半的结果（在本线程进行搜索），如果前一半没有找到才去检查后一半的结果。

并行化 std::partial_sum

方法一：每个线程各自负责一个 chunk

把数组分成 chunk，每个线程为一个 chunk 计算 partial sum（并行），然后不同线程通信得到上一 chunk 末尾的值 $x_{i-1}$（串行），最后每个线程各自给整个 chunk 加上 $x_{i-1}$（并行）。

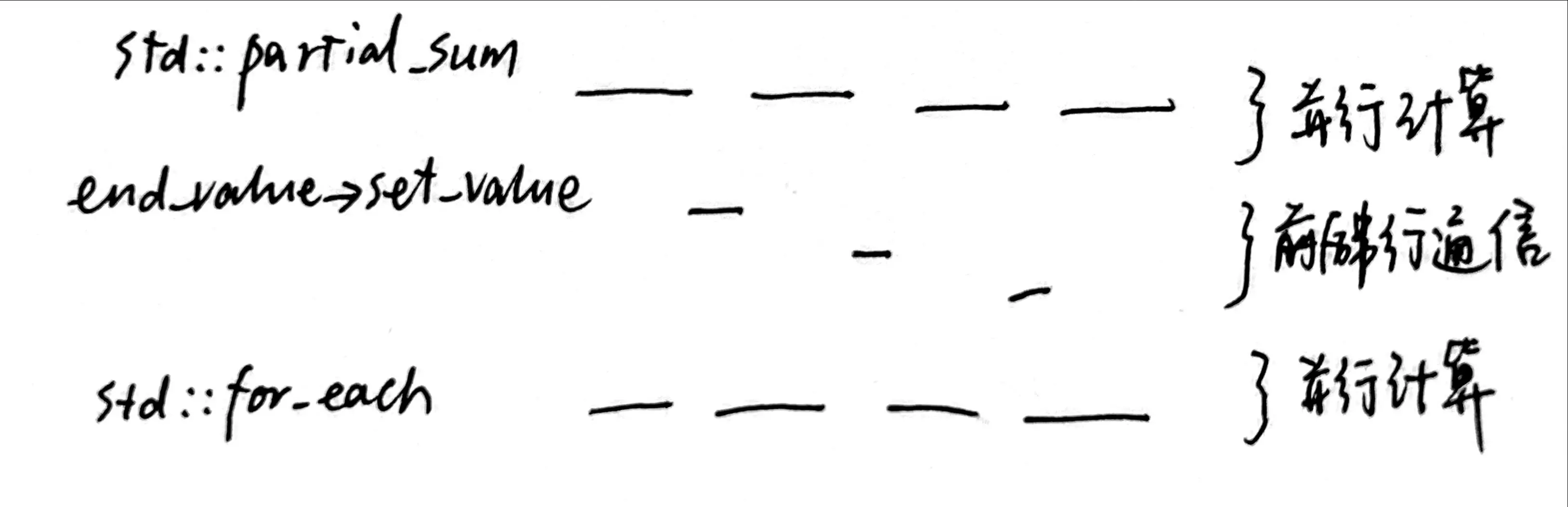
这个方法中相邻 chunk 通信是使用 std::promise 和 std::future 来完成的。图中有一点没有反映真实情况的是：只要当前线程将结果传给后面的线程了，就可以给自己负责的 chunk 中的每一个元素加上偏移，不需要整条链路的同步完成。

方法二：The incremental pairwise algorithm

This second approach to calculating the partial sums by adding elements increasingly further away works best where your processors can execute the additions in lockstep.

我记得 Programming Massively Parallel Processors 里面也讲过对折迭代，C++ Concurrency in Action 这里要在 CPU 上实现类似的算法。接下来把两本书介绍的算法进行比较。

两本书里面用的是什么算法？

Programming Massively Parallel Processors 先介绍了 Kogge-Stone 算法，然后介绍了更加高效的 Brent-Kung 算法。书上也提到了存在基于 warp shuffle 的更高效的算法，但是没有做详细介绍。

C++ Concurrency in Action 中的算法是 Kogge-Stone 算法。

Koggle-Stone 算法

在 Koggle-Stone 算法中，第一次迭代后前 2 个元素的 partial sum 已经算好，第二次迭代后前 4 个元素的 partial sum 已经算好，第三次迭代后前 8 个元素的 partial sum 已经算好……Koggle-Stone 算法的总操作数为 $N \mathit{log}_{2}(N) - (N - 1)$。因为在一个迭代中要读一次、写一次，所以在没有双缓冲的情况下一个迭代需要做两次同步。

Brent-Kung 算法

在 Brent-Kung 算法中，reduction tree 操作数为 $N-1$，reverse tree 操作数为 $N-1-\mathit{log}_2(N)$，总操作数为 $2N-2-\mathit{log}_2(N)$。

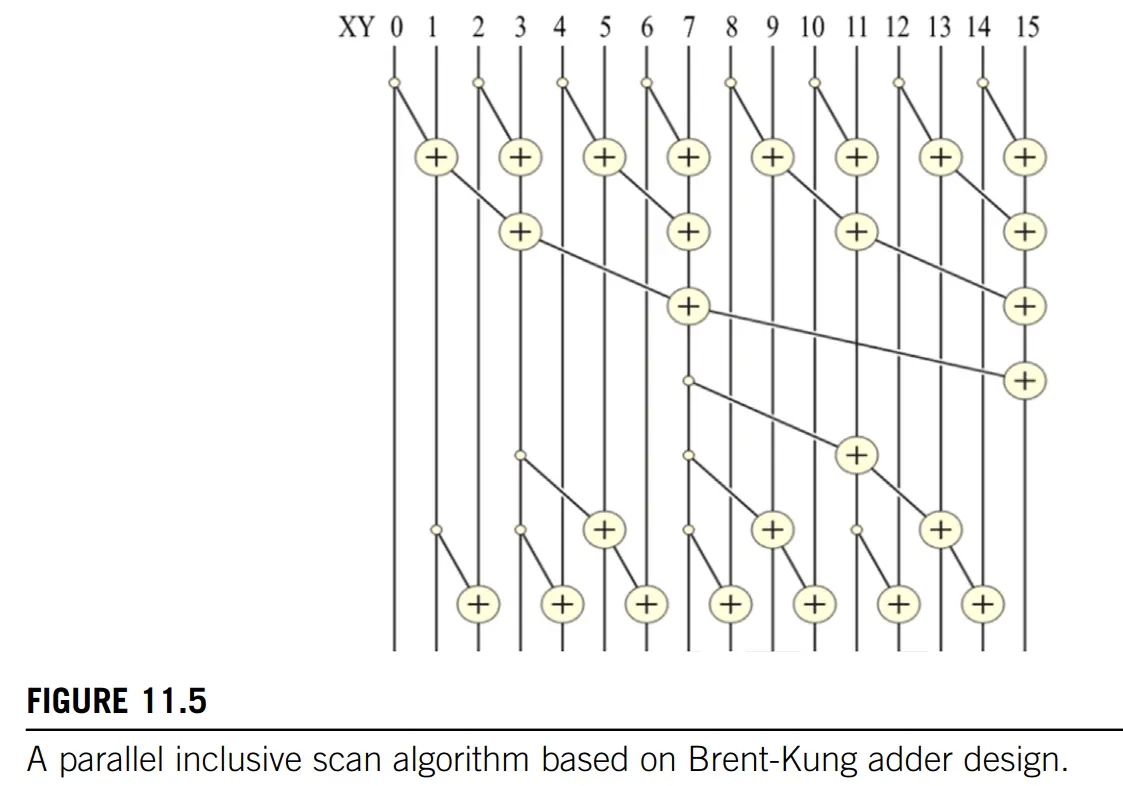
Reduction tree: （从 1 开始计数）2 的幂的位置的元素在 reduction tree 结束后可以得到最终的 partial sum。从下图中读写示意图来看，读的位置和写的位置并没有相互交错，所以一个迭代中只需要进行一次同步。

一种做法是让每个线程都处理对应位置上的元素，为其判断是否需要将 XY[i-stride] 的值加到 XY[i] 上面来。但是每个 warp 中有的线程不进 if，有的线程进 if，control divergence 比较多。

// blockDim.x 是分段扫描的数组段大小的一半，也就是说只要一半的线程就能计算该数组段
for(unsigned int stride = 1; stride <= blockDim.x; stride *= 2) {
    __syncthreads();
    // 这里对 (2 * stride) 取模而不是对 stride 取模，是因为算的是 inclusive scan，
    // 0 号元素并不需要进行叠加操作。
    if ((threadIdx.x + 1) % (2 * stride) == 0) {
        XY[threadIdx.x] += XY[threadIdx.x - stride];
    }
}

另一种做法是将工作线程集中到 block 头部的若干 warp 中，线程号（threadIdx.x 并不对应要处理的元素的下标号），这样做减少了控制分歧，性能更好。观察上图，如果下标从 1 开始，每一轮分别是 2 的倍数、4 的倍数、8 的倍数…… 下标处的元素参与计算。因此可以直接算出来第 $i$ 个会参与计算的下标是 $i * (2 * \mathit{stride})$，实际上数组下标从 0 计算、线程 ID（$i$）也从 0 开始，那么表达式就变成了 $(i+1) * (2 * \mathit{stride})-1$。最后做一下数组越界检查。

for(unsigned int stride = 1; stride <= blockDim.x; stride *= 2) {
    __syncthreads();
    int index = (threadIdx.x + 1) * 2 * stride - 1;
    if(index < SECTION_SIZE) { // 书中的 SECTION_SIZE 是对分段数组大小
        XY[index] += XY[index - stride];
    }
}

Reduction tree 结束之后，$\mathit{lowbit}(i+1)$ 能计算出 $XY[i]$ 已经包含了前面（含自己）几个数的和。令 $sum[-1] = 0$，有：

• 例子 1：如图，$XY[11]$ 是原 $XY[8...11]$ 的和。
• 例子 2：按照公式，所有从 1 计数的 2 的幂的位置都已经得到了最终 sum。

这其实完成了一个树状数组。

Reverse tree: 对于 $XY[i]$，我们希望把 $sum[i-\mathit{lowbit}(i+1)]$ 加回来。刚开始时只有满足 $i = 2^n-1(n=0,1,2...)$ 的 $XY[i]$ 和 $sum[i]$ 相等，所以只能把这些数作为加数往后加。（$XY[i]$ 是最终计算目标，而 $sum[i]$ 是当前计算结果。）

有一种方案可以满足所有元素的依赖关系：首先计算 $popcount(i+1)$ 小的那些元素 $XY[i]$，其中 popcount 操作表示对整数二进制表示中的 1 计数。图中 $XY[11]$ 和 $XY[5]$ 分别对应 12 号和 6 号，他们都只有 6 位，计算是可以同时进行的。这种方法还是从线程 $i$ 对应下标 $i$ 的角度来思考的，不仅需要调用 $popcount()$ 函数，还有控制分歧。书上给出了一种效率更高的、基于 stride 倍减的向后叠加算法，在满足计算依赖的情况下保持了代码简单。

最终代码。书上还进行了“线程减半”的优化：虽然每个块处理了一块大小为 SECTION_SIZE 的内存区域，但是实际上使用的线程数最多为 SECTION_SIZE/2（可以看上面的图，斜线表示数据操作，每一行斜线都不超过元素总数的一半），所以在启动 kernel 的时候给的块内线程数只要 SECTION_SIZE/2 就行。换句话说，如果想要减少段数（增大段大小），可以将块内线程数开满，并将 SECTION_SIZE 设置为它的 2 倍。

__global__ void Brent_Kung_scan_kernel(float *X, float *Y, unsigned int N) {
    __shared__ float XY[SECTION_SIZE];
    unsigned int i = 2*blockIdx.x*blockDim.x + threadIdx.x;
    // 有 SECTION_SIZE == 2 * blockDim.x。
    // 下面将 X 的数据加载到共享内存中以加快访问。看上去复杂了一点，实际上只是因为
    // 现在一个 SECTION_SIZE 等于两倍块内线程数，所以需要多做一些处理。
    if(i < N) XY[threadIdx.x] = X[i];
    if(i + blockDim.x < N) XY[threadIdx.x + blockDim.x] = X[i + blockDim.x];
    // Reduction tree.
    for(unsigned int stride = 1; stride <= blockDim.x; stride *= 2) {
        __syncthreads();
        unsigned int index = (threadIdx.x + 1)*2*stride - 1;
        if(index < SECTION_SIZE) {
            XY[index] += XY[index - stride];
        }
    }
    // Reverse tree.
    for (int stride = SECTION_SIZE/4; stride > 0; stride /= 2) {
        __syncthreads();
        unsigned int index = (threadIdx.x + 1)*stride*2 - 1;
        if(index + stride < SECTION_SIZE) {
            XY[index + stride] += XY[index];
        }
    }
    __syncthreads();
    // 将共享缓存上的结果写回结果数组。
    if (i < N) Y[i] = XY[threadIdx.x];
    if (i + blockDim.x < N) Y[i + blockDim.x] = XY[threadIdx.x + blockDim.x];
}

注意到 Brent-Kung 算法每个迭代只同步一次。

双缓冲

使用 Kogge-Stone 算法时，GPU 和 CPU 都能使用双缓冲提高效率。C++ Concurrency in Action 示例使用了一个输入区间一样大的工作区，然后和输入区间轮替保存每次迭代的结果。线程们通过全局双缓冲区共享数据，而不是各自用变量暂存要写入的结果，将每个迭代要同步的次数从 2 次减少到了 1 次。

使用 Brent-Kung 算法时，不需要双缓冲，每个迭代只同步 1 次。

Barrier 的使用

无论是 GPU 上的计算还是 CPU 上的计算，都要用 barrier 来同步。CUDA 中直接使用 __syncthreads() 就好，而 CPU 算法要使用 std::barrier。由于 std::barrier 在 C++20 才被加入，书上给了一个简单的基于原子变量的忙等待的实现。

线程的提前退出

CUDA 中 __syncthreads() 不会让参与同步的 GPU 线程退出，而 C++ std::barrier 允许当前线程用 arrive_and_drop() 来退出同步，这一方面是因为在 CPU 上计算可以控制更加精细，另一方面是因为操作系统的线程资源很宝贵，有必要及时释放。参考下面两份代码（忽略是否使用双缓冲这一点的差异）：

CUDA 中的 Koggle Stone 算法：

__global__ void Kogge_Stone_scan_kernel(float *X, float *Y, unsigned int N) {
    __shared__ float XY[SECTION_SIZE];
    unsigned int i = blockIdx.x * blockDim.x + threadIdx.x;

    if (i < N) {
        XY[threadIdx.x] = X[i];
    } else {
        XY[threadIdx.x] = 0.0f;
    }

    // 注意 stride < blockDim.x 保证了所有线程要经历相同的迭代次数
    for (unsigned int stride = 1; stride < blockDim.x; stride *= 2) {
        __syncthreads();
        float temp;
        if (threadIdx.x >= stride) {
            temp = XY[threadIdx.x] + XY[threadIdx.x - stride];
        }
        __syncthreads();
        if (threadIdx.x >= stride) {
            XY[threadIdx.x] = temp;
        }
    }

    if (i < N) {
        Y[i] = XY[threadIdx.x];
    }
}

C++ 中的 Koggle Stone 算法（有线程提前退出 barrier）：

void operator()(Iterator first, Iterator last, 
                std::vector<value_type>& buffer, unsigned i, barrier& b) {
    value_type& ith_element = *(first + i);
    bool update_source = false;

    // stride <= i 而不是 stride < std::distance(first, last)
    // 使得不同线程的迭代次数不同，有些线程比其他线程更早离开循环
    for (unsigned step = 0, stride = 1; stride <= i; ++step, stride *= 2) {
        value_type const& source = (step % 2) ? buffer[i] : ith_element;
        value_type& dest = (step % 2) ? ith_element : buffer[i];
        value_type const& addend = (step % 2) ? buffer[i - stride] : *(first + i - stride);

        dest = source + addend;
        update_source = !(step % 2);
        b.wait(); // 相当于 std::barrier::arrive_and_wait
    }

    if (update_source) {
        ith_element = buffer[i];
    }
    // 必须离开线程组，否则其他线程会卡在 lockstep 中
    b.done_waiting(); // 相当于 std::barrier::arrive_and_drop
}

Segmented scan 和 stream-based scan

C++ Concurrency in Action 示例对每个元素专门创建了一个线程（代码简单但效率低），尽管系统内的线程数有上限（在我的 wsl2 中，cat /proc/sys/kernel/threads-max 结果为 125610），但这仍然比 CUDA 中允许的一个 block 中的最大线程数 1024 要多，因此实现的是一个不分段的 scan 算法，或者说没有对数据量极大的情况做分段处理。

在 GPU 上，因为一个 block 中线程数量有限，可以：①先做分段的 scan（无论是 inclusive 还是 exclusive），在最后一步中将每个段的元素总和（block sums）写回到一个辅助数组中；②对 block sums 做 exclusive scan，得到每个 block 上应该加多少值作为补偿；③将这些值加回到第 ① 步算出来的结果上。

如果要在 GPU 上避免分段，可以借用“Chunks 之间通信”的思路实现一趟的算法。这样可以避免先将中间结果写到全局内存再读取的开销。这被称为 stream-based scan algorithm。Programming Massively Parallel Processors 中介绍了以原子变量来同步的方法：

__shared__ float previous_sum;
if (threadIdx.x == 0){
    // Wait for previous flag
    while(atomicAdd(&flags[bid], 0) == 0) { }
    // Read previous partial sum
    previous_sum = scan_value[bid];
    // Propagate partial sum
    scan_value[bid + 1] = previous_sum + local_sum;
    // Memory fence
    __threadfence();
    // Set flag
    atomicAdd(&flags[bid + 1], 1);
}
__syncthreads();

上面这种方法有个问题是：GPU 上块并不是（按照 blockIdx.x）先后执行的，有可能前一个块没有被执行，而后一个块开始执行了。这样可能导致性能下降或者死锁。书上说如果 block i 到 i+N 占用了所有的 SM，那么 block i-1 不能得到调度，block i 到 i+N 只能无限等待下去。

一种补救的办法是 dynamic block index assignment，也就是不使用 blockIdx.x，而是通过原子变量来动态获取 block 编号：

__shared__ unsigned int bid_s;
if (threadIdx.x == 0) {
    bid_s = atomicAdd(blockCounter, 1);
}
__syncthreads();
unsigned int bid = bid_s;